Análise de Fourier e Conteúdo Harmônico
Análise de Fourier e Conteúdo Harmônico
10/NOV/2021
Seção 1: Introdução
De acordo com a teoria inicialmente concebida pelo matemático e físico francês Jean-Baptiste Joseph Fourier, os sinais periódicos, de forma geral, podem ser representados por uma série infinita de termos em senos e cossenos, em frequências múltiplas inteiras (harmônicas) da frequência do sinal periódico original (frequência fundamental). As séries obtidas por Fourier restringiam-se a funções com valores reais (aqui o termo real se refere ao conjunto dos números Reais, contrapondo-se ao conjunto de números Complexos), e com argumentos reais. Desde essa época, muitas novas abordagens permitiram melhor definir e compreender as séries de Fourier. Muitas dessas abordagens se baseiam em técnicas e ferramental matemático ainda não disponíveis, quando do trabalho desenvolvido por Fourier. Se você deseja se aprofundar nos conceitos matemáticos relacionados às séries de Fourier, o Lathi é sempre um bom ponto de partida. Neste texto, pretendo usar uma abordagem mais qualitativa, ainda que tomando por base uma "âncora" matemática.
A seguir, apresenta-se o ferramental matemático utilizado para gerar a série de Fourier:

Figura 1 - Expressão gereal da Série de Fourier
Tal como concebida originalmente, a série de Fourier apresenta uma expressão matemática para os termos de cada uma dessas parcelas. Como se nota, a partir de uma função periódica f(x), pode-se obter uma série matemática (de Fourier) que representa de forma exata a função periódica original. Deve-se compreender que para cada sinal periódico analisado com o ferramental disponibilizado por Fourier, vai-se obter uma expressão matemática correspondente ao sinal periódico sob análise. Além da modelagem matemática de um sinal físico, a abordagem permite também a análise do sinal periódico numa perspectiva distinta da sua evolução temporal: a análise harmônica, permitindo construir a chamada resposta em frequência.
Como se pode inferirir, a expressão matemática obtida conterá diversas parcelas em senos e cossenos, ocorrendo em múltiplas frequências distintas. É razoável compreender que dois sinais distintos apresentarão evolução temporal distintas e, numa perspectiva da análise de Fourier, apresentarão expressões matemáticas distintas. Da mesma forma, suas representações harmônicas serão igualmente distintas.
A seguir, a título de ilustração, mostram-se algumas importantes formas de onda periódicas, amplamente usadas em eletrônica e telecomunicações. Para cada uma delas, vai-se mostrar a expressão obtida com o ferramental matemático de Fourier, e a sua representação gráfica, em função da quantidade de harmônicos utilizados.
Seção 2: Representação de Onda Quadrada com a Série de Fourier
Inicialmente vamos focar na onda quadrada. Como se sabe, esta forma de onda é muito importante, sendo utilizada como:
- Sinal de "relógio" ("clock"), na sincronização de circuitos digitais;
- Sinal de portadora, para a comunicação digital;
- Transmissão de energia, em circuitos de potência.
Cabe notar que o termo "quadrado" é utilizado para indicar um sinal cuja duração no pico superior é igual à duração no pico inferior. Uma vez que o eixo vertical indica amplitudes, apresentadas em diversas grandezas distintas, e o eixo horizontal indica o tempo, o termo mais adequado, para esse tipo de sinal, seria o de onda "retangular". Entretanto, vai-se manter o termo "quadrado", por ser esse o mais comum. Evidentemente, as diversas aplicações deste tipo de onda podem requerer alterações nas características de tempo desta onda. A despeito disso, o estudo desse tipo de onda se mantém importante e relevante. A Figura 2(a) apresenta a onda quadrada a ser estudada a seguir:
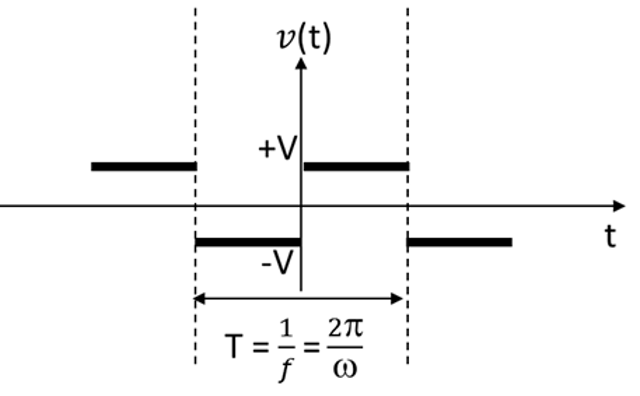
Figura 2(a) - Onda Quadrada
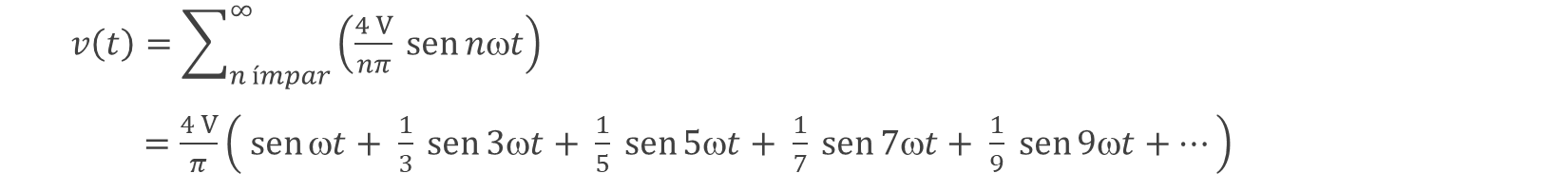
Figura 2(b) - Expressão de Fourier para a Onda Quadrada
Como se nota na Figura 2(b), a expressão matemática resultante para a onda quadrada de frequência f (ou ω=2πf), mostrada na Figura 2(a), apresenta apenas termos em senos, e ocorrendo apenas em frequências múltiplas ímpares da frequência f (ou ω=2πf) original. A frequência f (ou ω=2πf) da forma de onda original é chamada de frequência fundamental e os seus diversos múltiplos são chamados de frequências harmônicas. É importante notar que a própria frequência fundamental também é um harmônico e eventualmente chamada de "primeiro harmônico". Numa linguagem mais técnica, pode-se dizer que a onda quadrada mostrada na Figura 2(a) só apresenta harmônicos ímpares e é formada apenas por senos. Isto acontece porque tanto os termos em cosseno, quanto os termos em seno com harmônicos pares, têm, todos eles, amplitudes nulas. Para se convencer disso, você terá que realizar as integrais indicadas na Figura 1 😄.
Assim, uma onda quadrada na frequência f = 1KHz é formada por harmônicos (no caso, apenas termos em seno) nas frequências de 1KHz, 3KHz ( 3f = 3 x 1KHz), 5KHz (5f = 5 x 1KHz), 7KHz (7f = 7 x 1KHz), e todos os harmônicos ímpares posteriores. Pode-se notar, na expressão matemática da Figura 2(b), que as amplitudes dos harmônicos de ordem elevada são menores que as dos harmônicos de ordem mais baixa. Isto porque, como pode ser visto na expressão, um harmônico de ordem "n", terá a sua amplitude multiplicada por 1/n.
Deve ser compreendido que a representação PERFEITA de uma onda quadrada terá de contar com infinitos harmônicos. De fato, quanto maior o número de harmônicos empregados na expressão matemática, mais o sinal resultante se parece com uma onda quadrada. A Figura 2(c) mostra a representação gráfica da expressão mostrada na Figura 2(b), considerando-se todos os harmônicos de 1 a 131. De fato, embora a representação obtida seja muito semelhante a uma onda quadrada, ela apresenta alguns "picos" nas bordas de transição. Esses "picos" tendem a desaparecer quando se utilizam mais harmônicos para a representação do sinal.
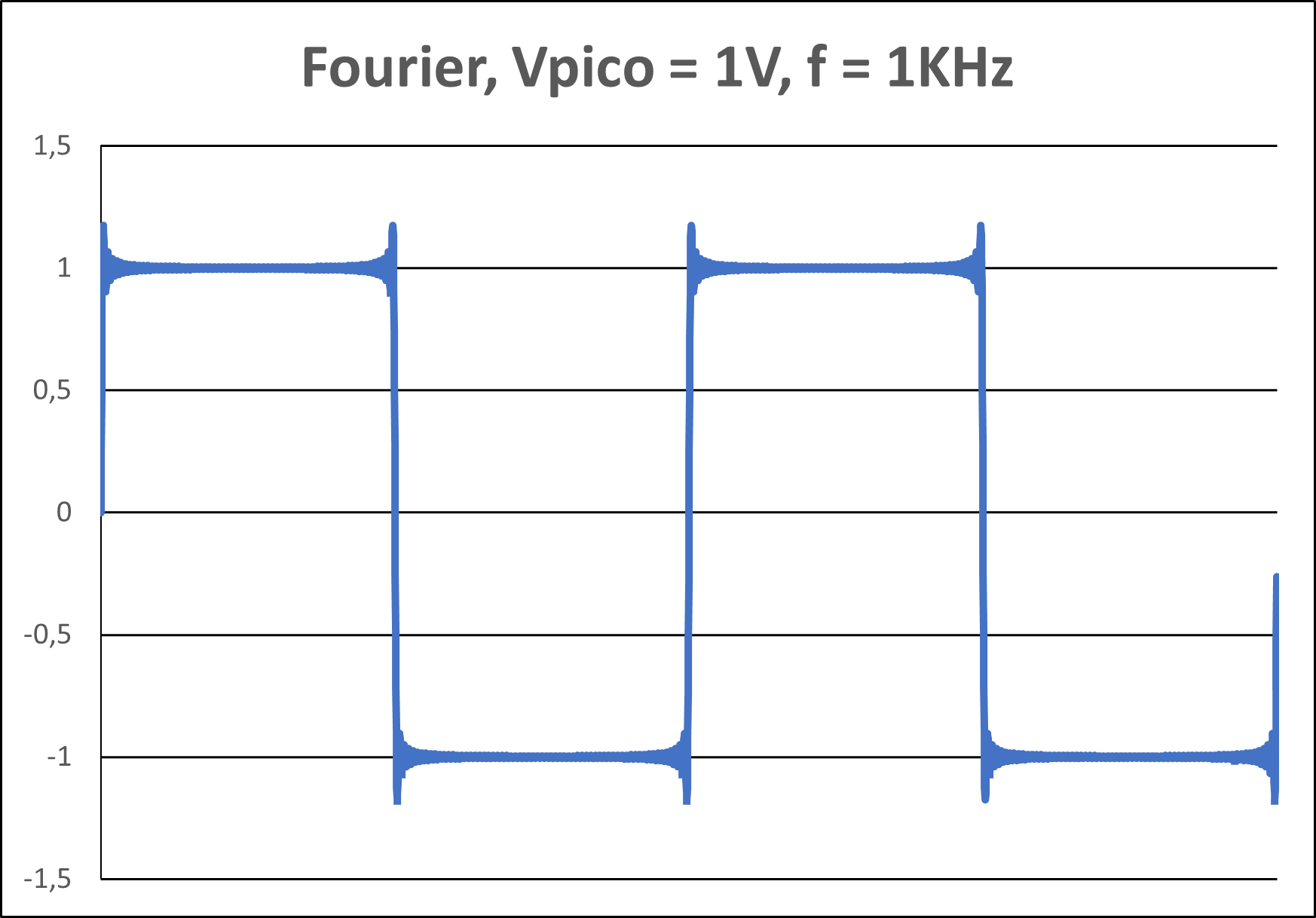
Figura 2(c) - Representação gráfica com 131 harmônicos
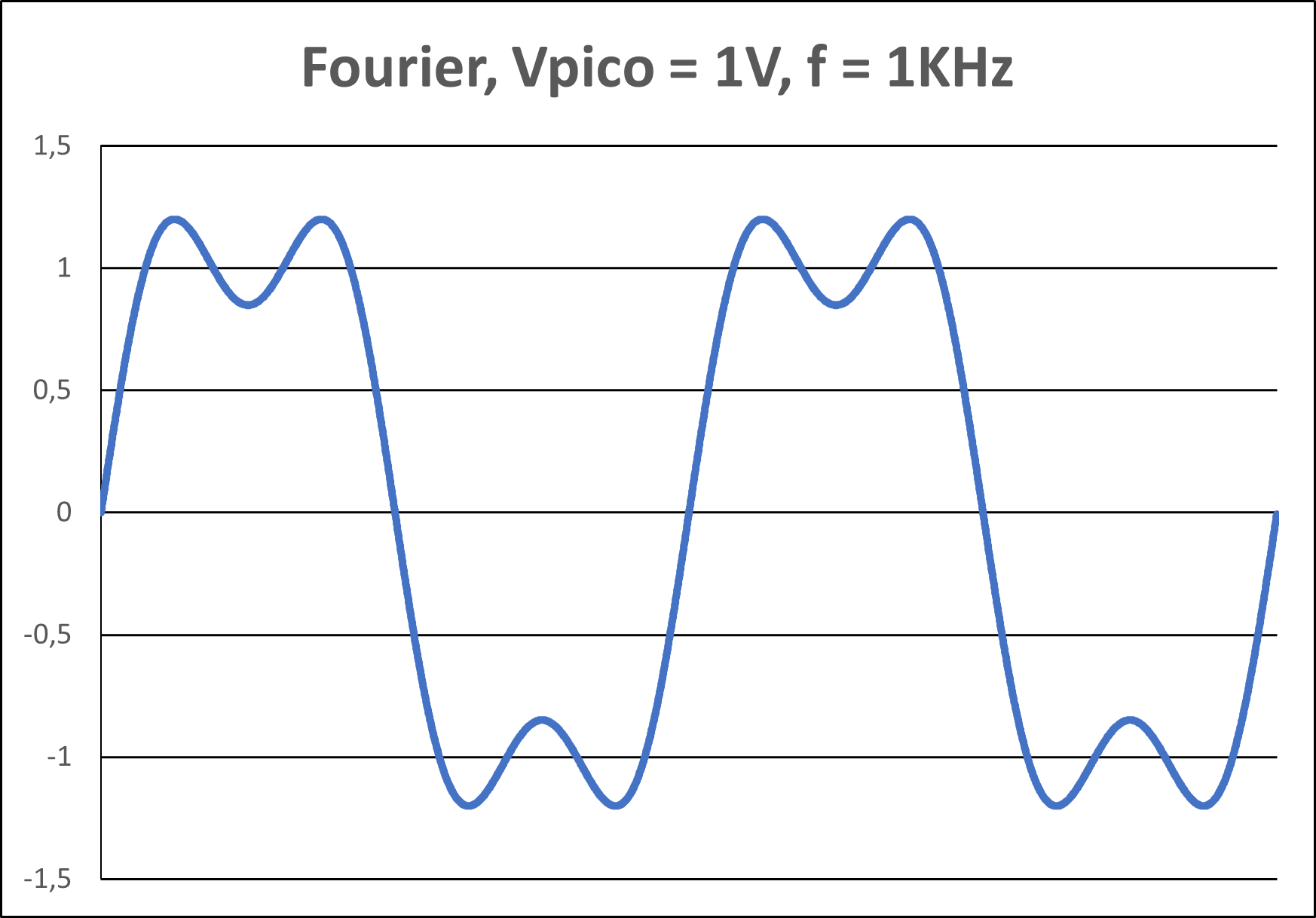
Figura 2(d) - Representação gráfica com 3 harmônicos
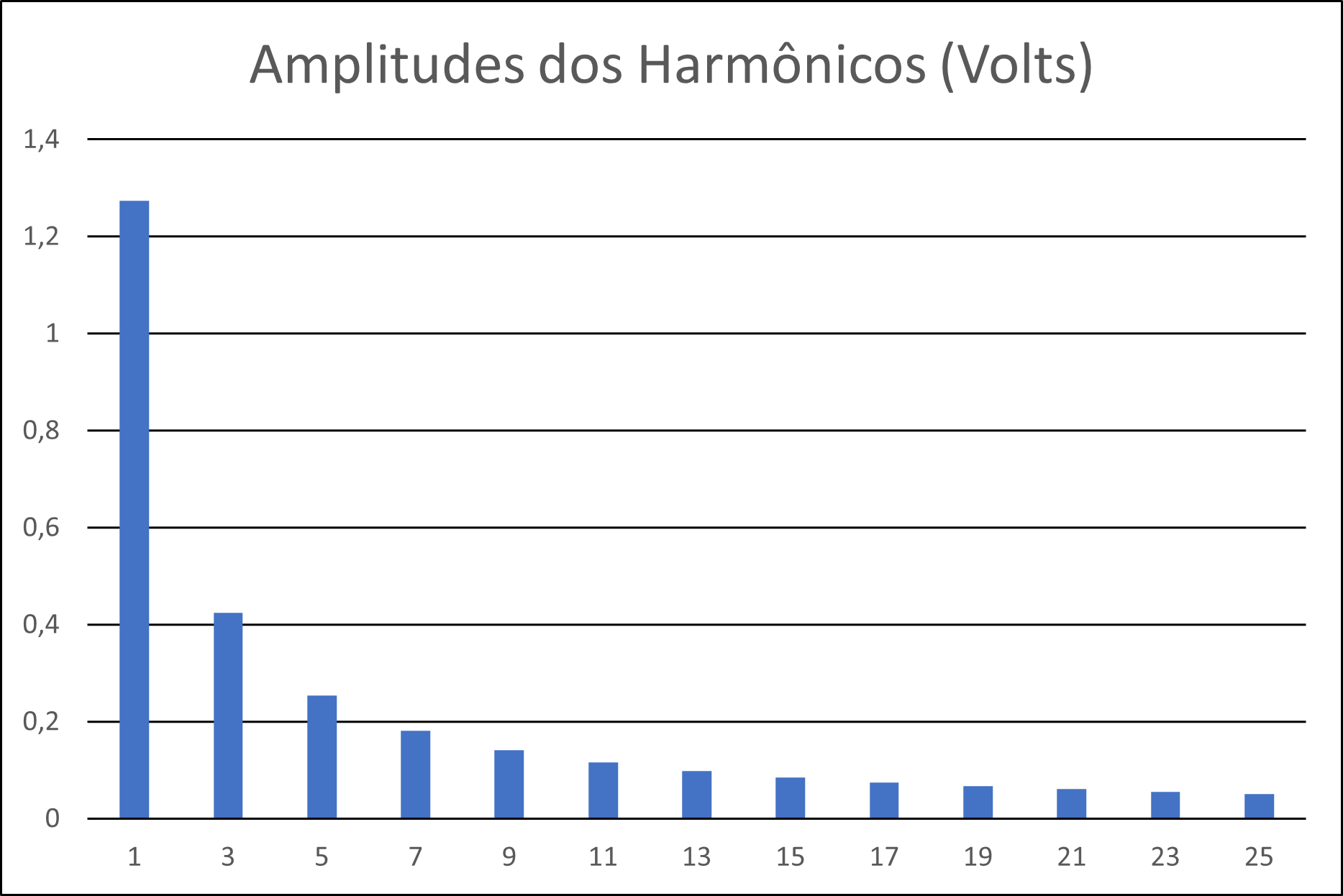
Figura 2(e) - Distribuição dos 25 primeiros harmônicos e suas amplitudes
Por outro lado, ao reduzir a quantidade de harmônicos na expressão, o sinal vai se tornando mais "arredondado", embora ainda mantenha alguma semelhança com a onda quadrada. A Figura 2(d) mostra a a representação gráfica da expressão matemática mostrada na Figura 2(b), incluindo-se apenas os 3 primeiros harmônicos (efetivamente apenas o primeiro e o terceiro harmônico, já que o segundo harmônico, que é par, é nulo). No limite, seria possível representar a onda quadrada com apenas um harmônico - o primeiro. Evidentemente, é a aplicação desejada para a onda quadrada que vai determinar a quantidade de harmônicos a serem considerados na sua representação. Embora, em alguns casos, um conteúdo harmônico mais pobre não chegue a prejudicar a inteligibilidade da informação, em outros, a falta dos harmônicos pode simplesmente impedir a compreensão do sinal.
É importante compreender que quanto mais harmônicos são considerados na expressão, mais "fiel" se torna a expressão matemática resultante. Da mesma forma, mais a sua representação gráfica se aproxima do sinal original. Evidentemente, os harmônicos de ordem mais alta apresentarão amplitudes muito baixas. Isto pode ser visto na Figura 2(e). Do ponto de vista da potência total do sinal, é razoável inferir também que a potência total dos harmônicos de ordem mais alta é bastante menor que a potência dos harmônicos de ordem mais baixa. De fato, a maior parte da potência do sinal se concentra nos harmônicos de ordem baixa. Por outro lado, são exatamente os harmônicos de ordem mais alta os responsáveis pelo aspecto "quadrado" da onda. Sem eles, sinal resultante "perde" a sua característica "brusca" e vai se tornando mais "arredondado". Assim, os harmônicos de ordem elevada são os responsáveis pelo comportamento mais brusco das ondas quadradas - ao menos é isso que se espera de uma onda que se chama de quadrada 😄.
A seguir mostram-se as figuras afins a outros tipos de ondas.
Seção 3: Representação de Onda Triangular com a Série de Fourier
A Figura 3 mostra os resultados para uma onda triangular.
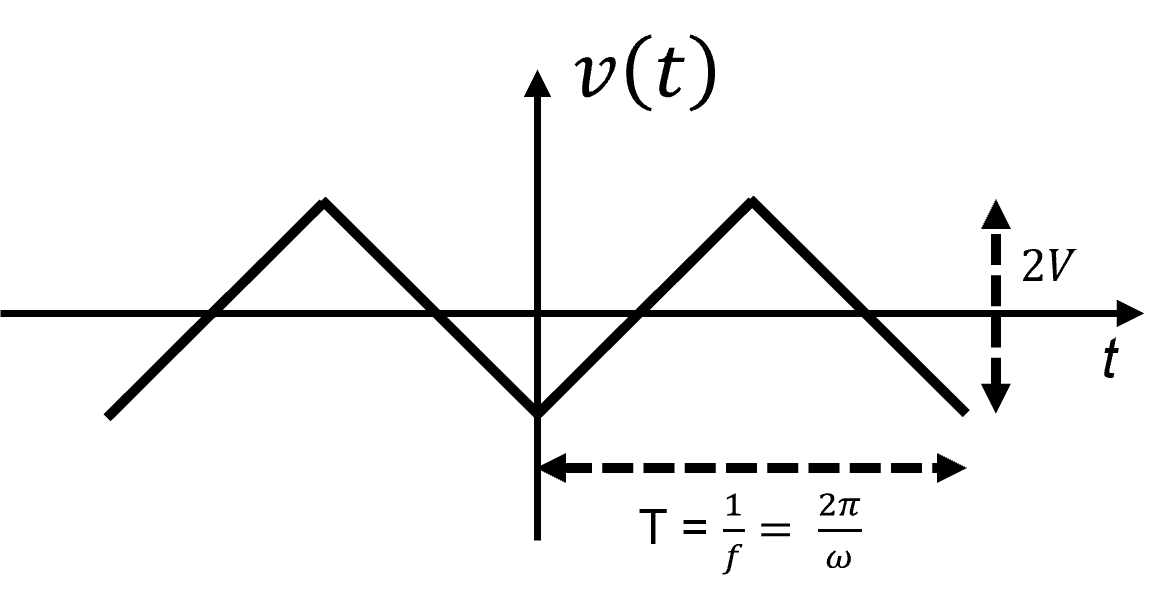
Figura 3(a) - Onda triangular
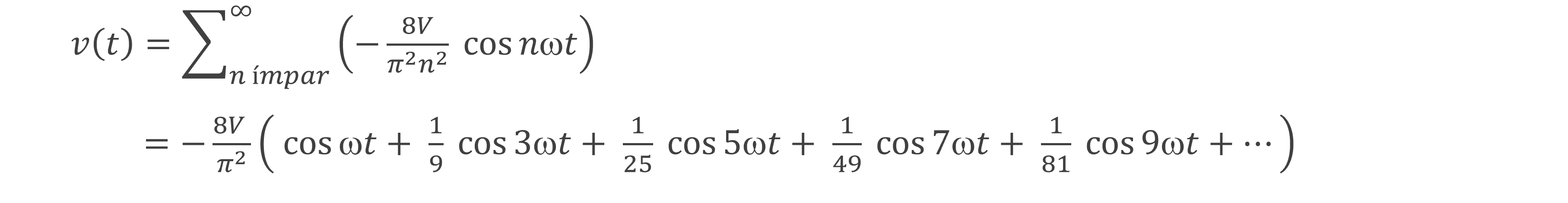
Figura 3(b) - Expressão de Fourier para a Onda Triangular
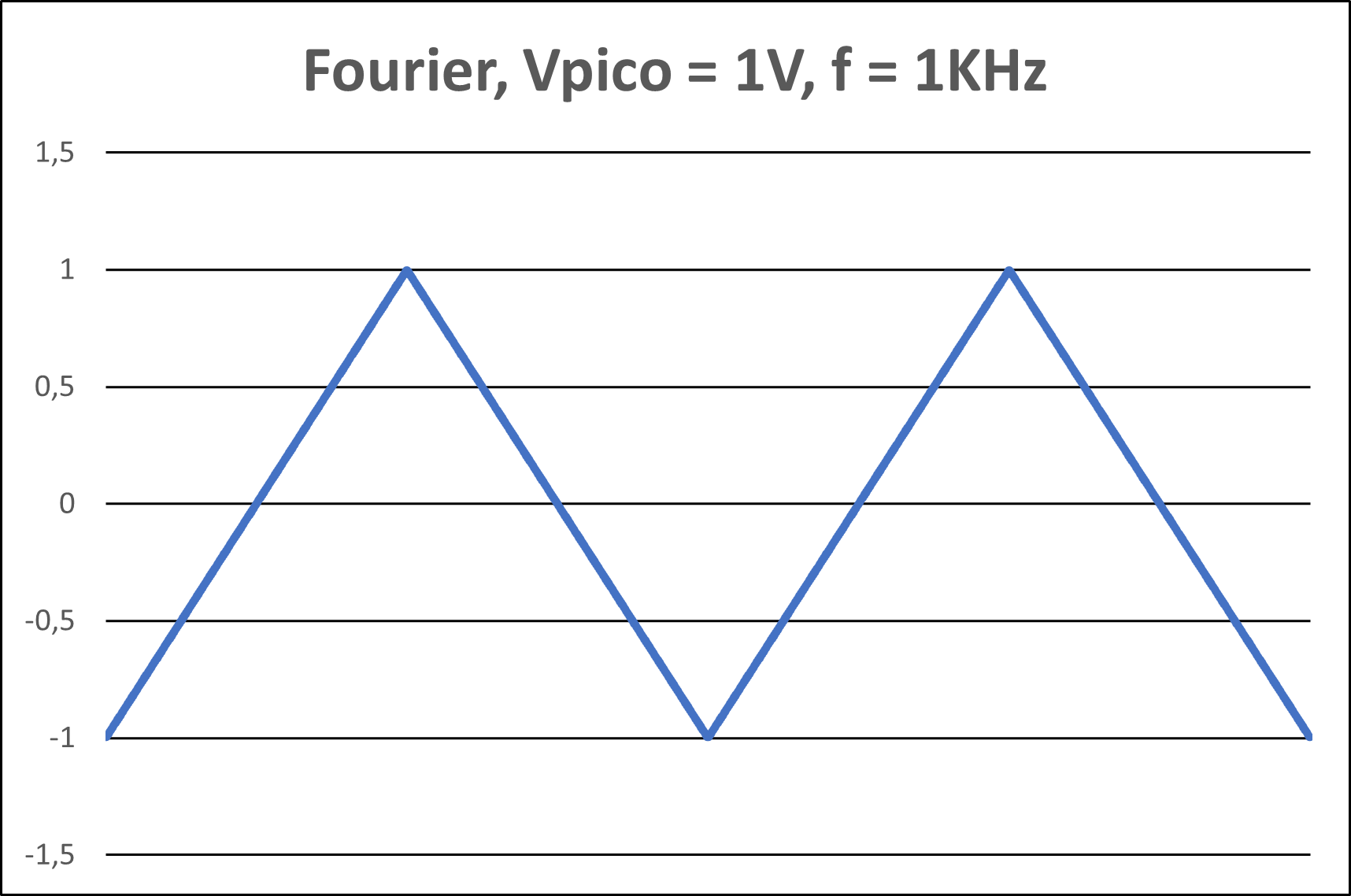
Figura 3(c) - Representação gráfica com 131 harmônicos
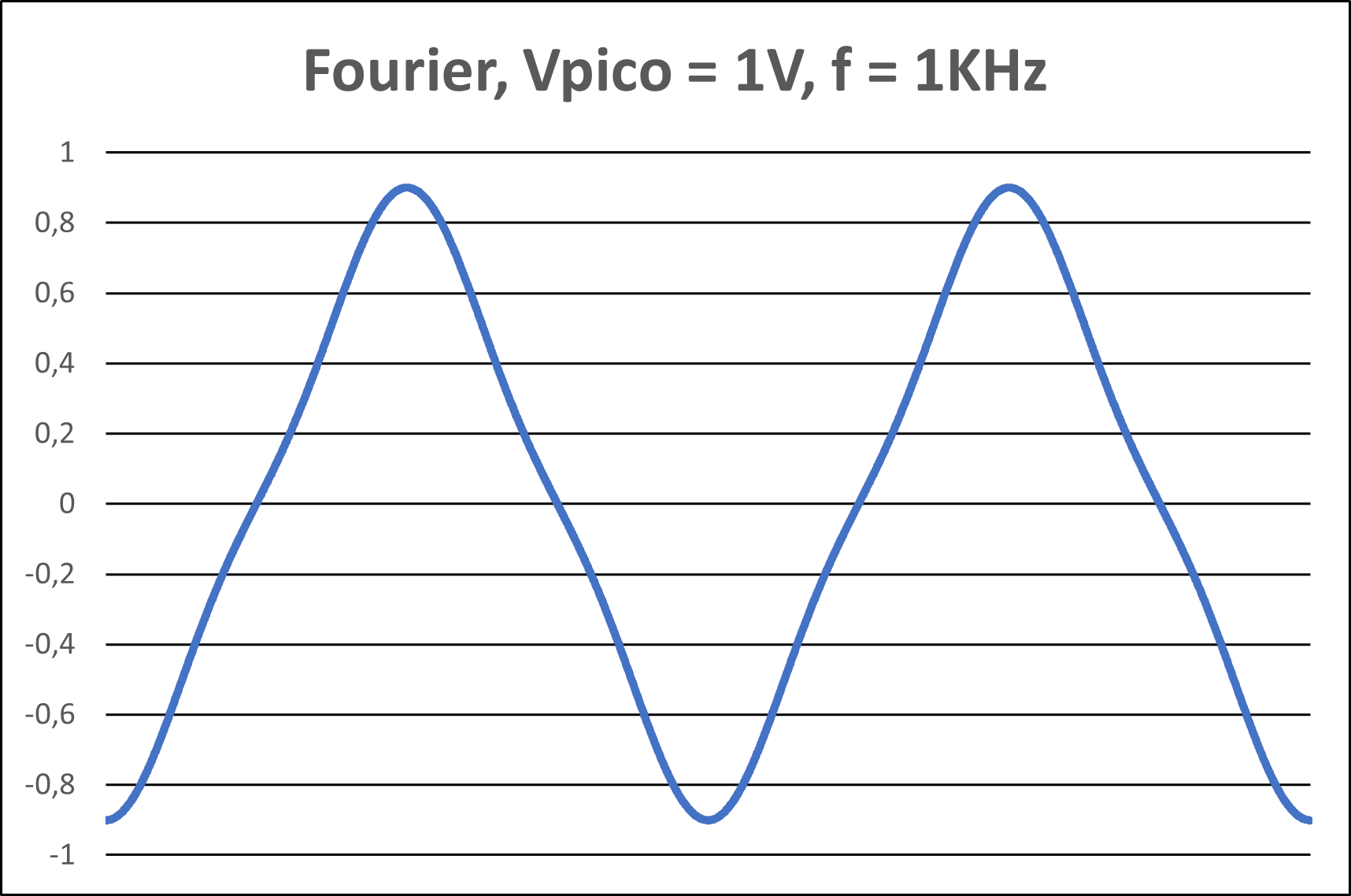
Figura 3(d) - Representação gráfica com 3 harmônicos
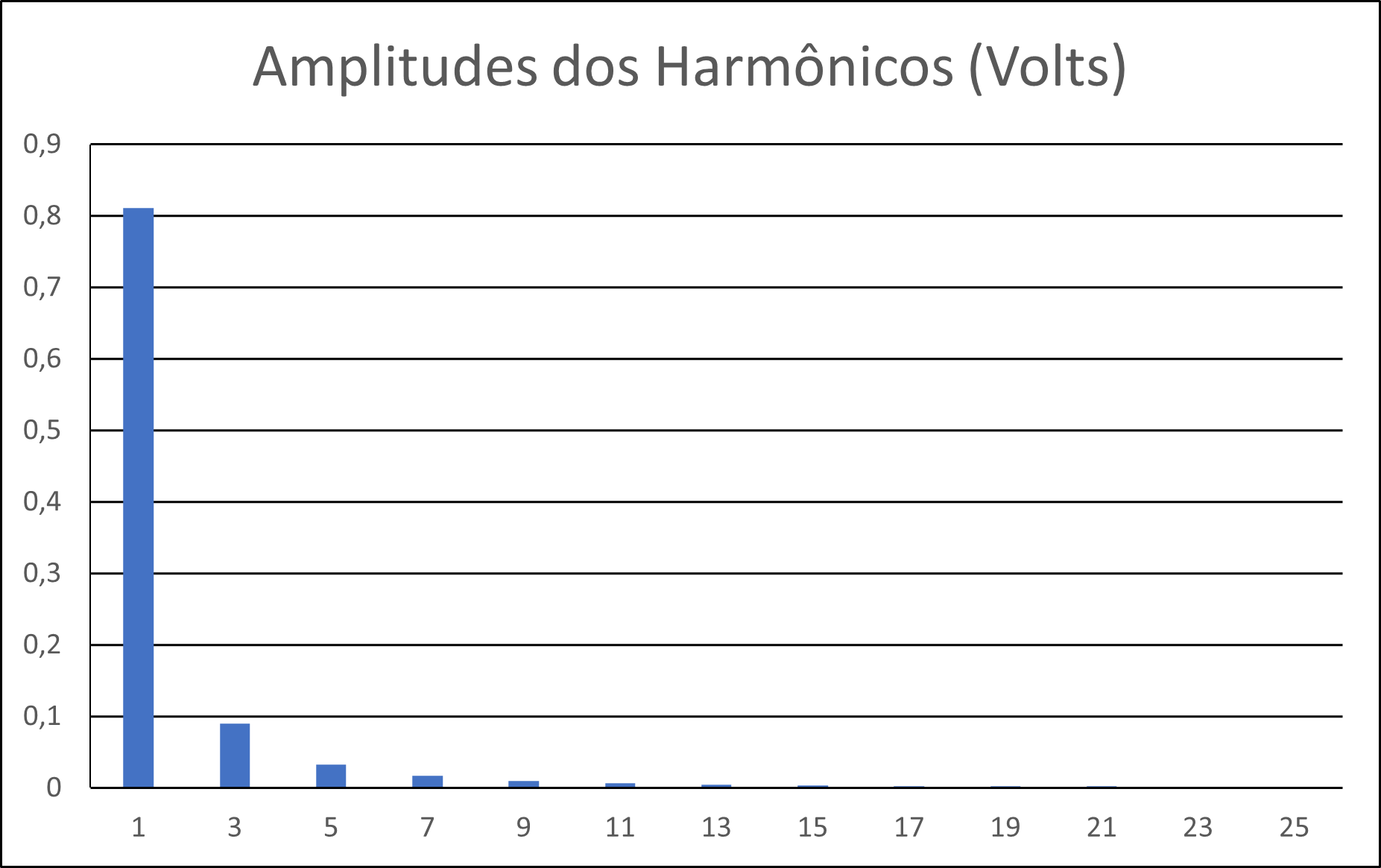
Figura 3(e) - Distribuição dos 25 primeiros harmônicos e suas amplitudes
Seção 4: Representação de Onda "Dente de Serra" com a Série de Fourier
A Figura 4 mostra os resultados para onda tipo "Dente de Serra".
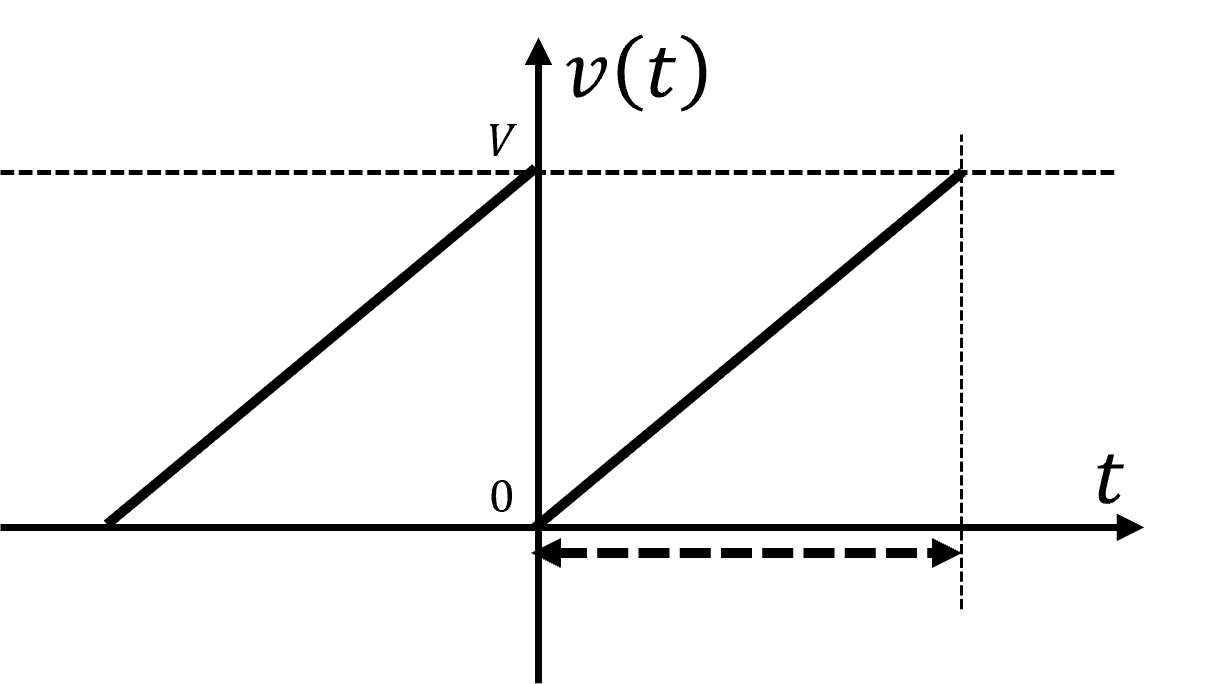
Figura 4(a) - Onda "Dente de Serra"
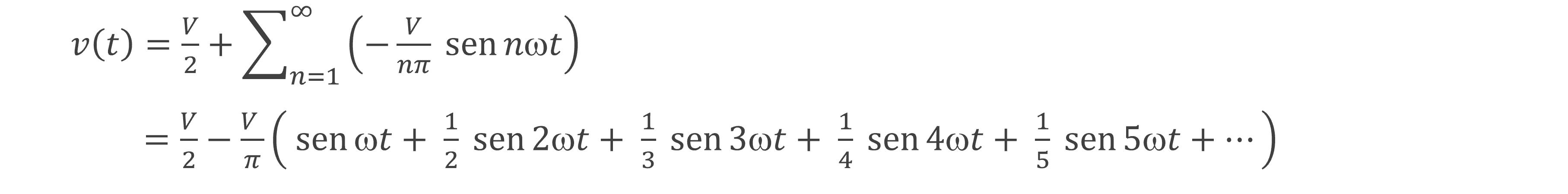
Figura 4(b) - Expressão de Fourier para a Onda "Dente de Serra"
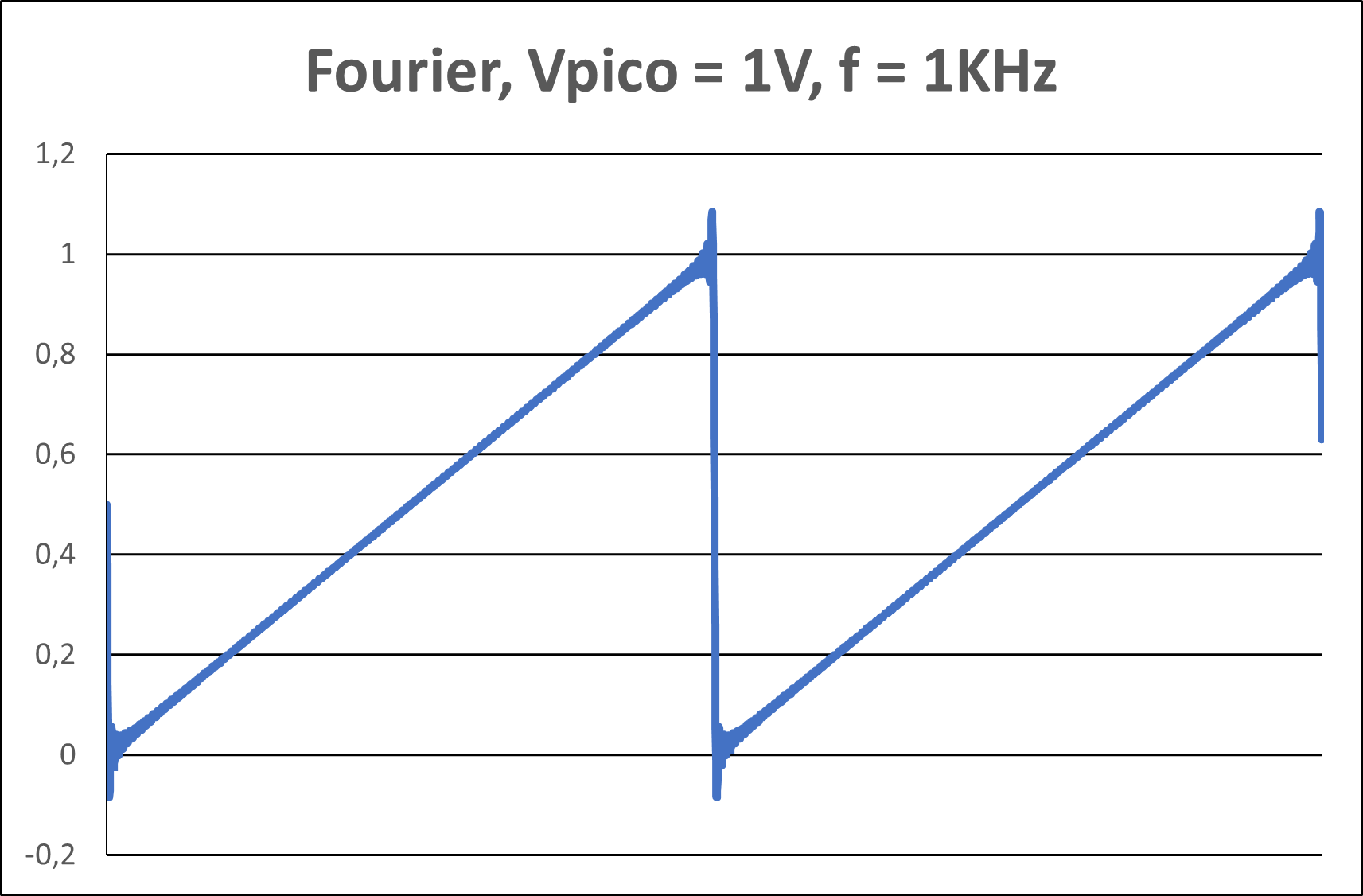
Figura 4(c) - Representação gráfica com 131 harmônicos
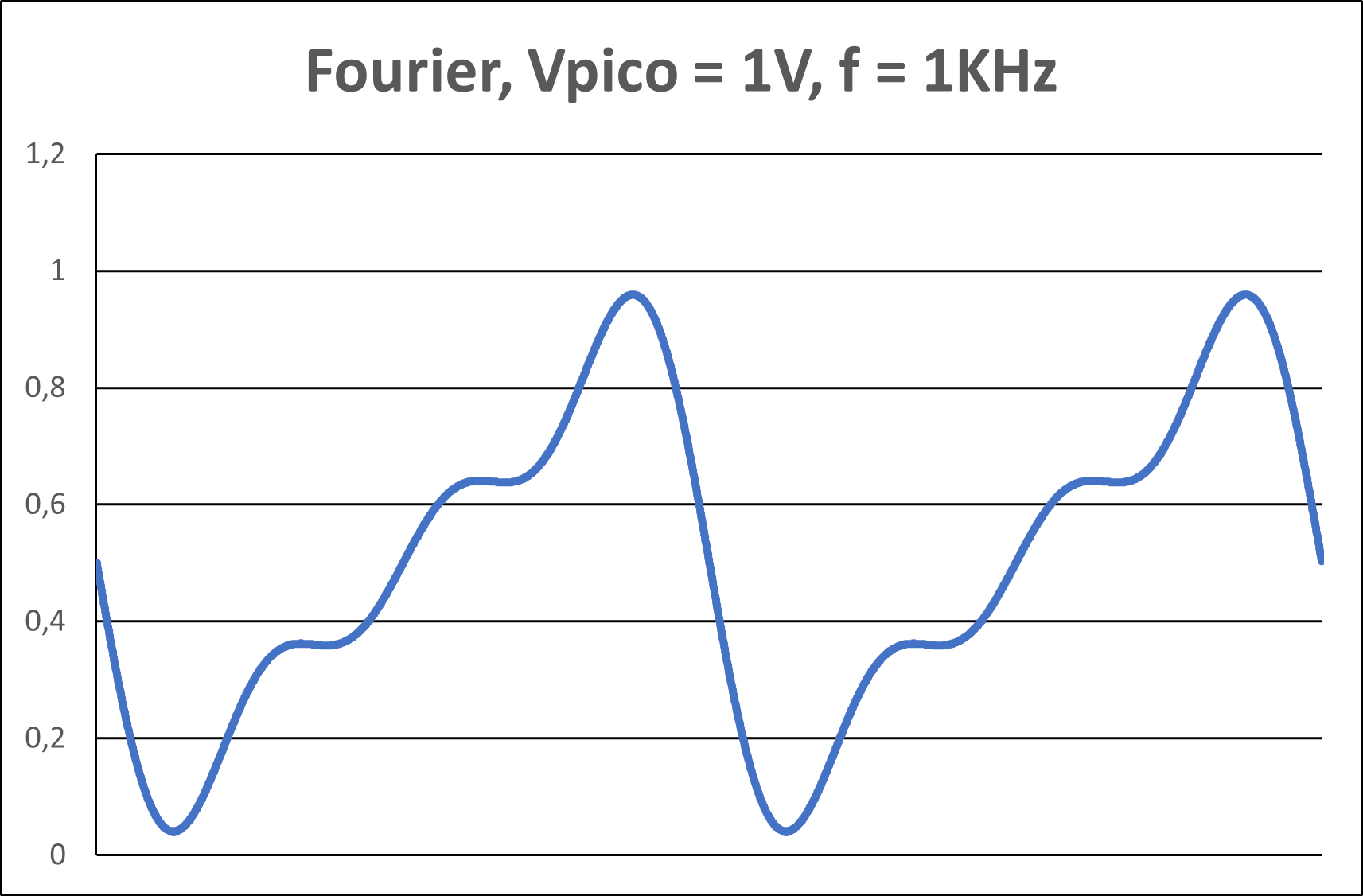
Figura 4(d) - Representação gráfica com 3 harmônicos
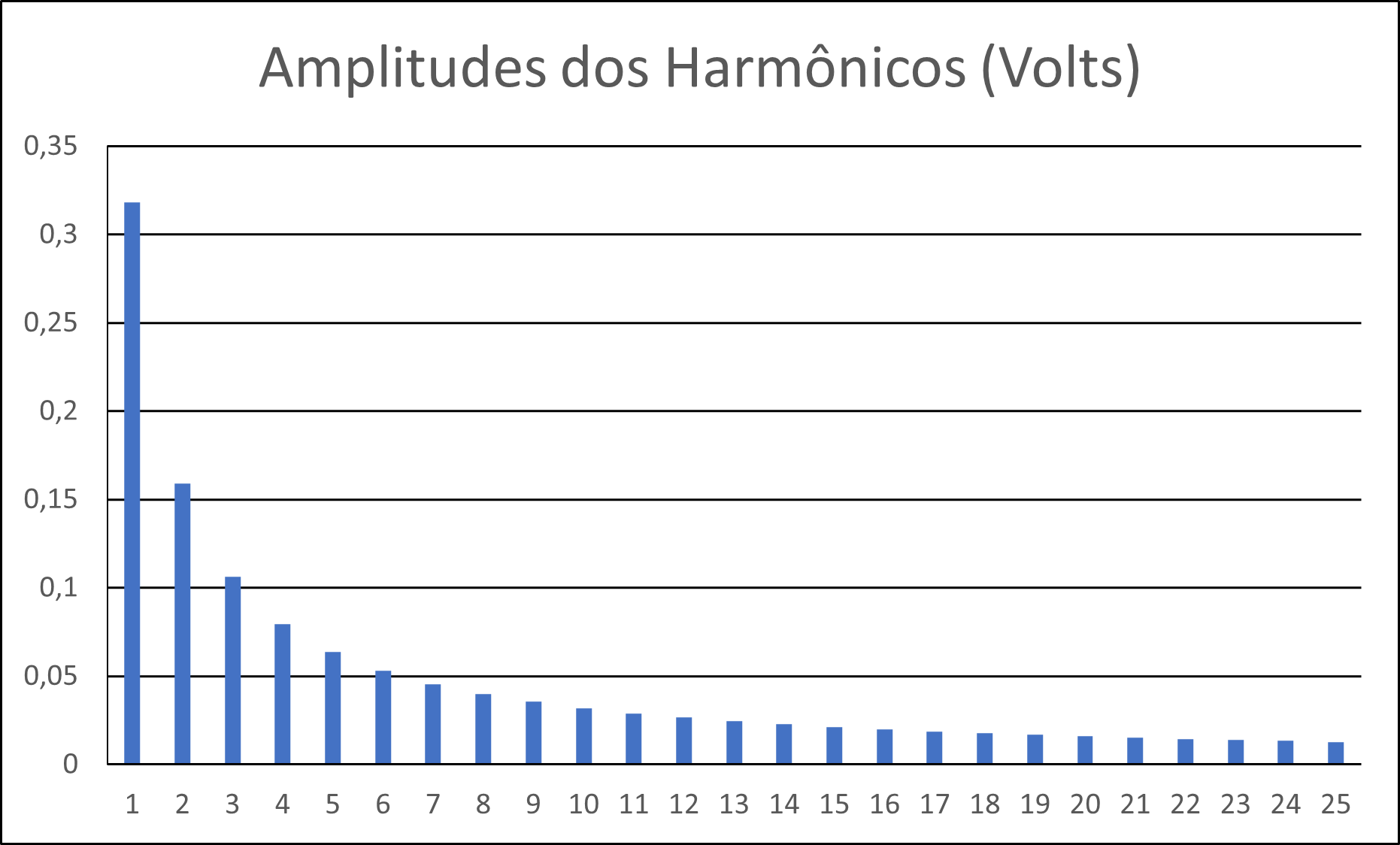
Figura 4(e) - Distribuição dos 25 primeiros harmônicos e suas amplitudes
Seção 5: Representação de um Sinal Pulsado com a Série de Fourier
Finalmente, a Figura 5 mostra os resultados para um trem de pulsos.
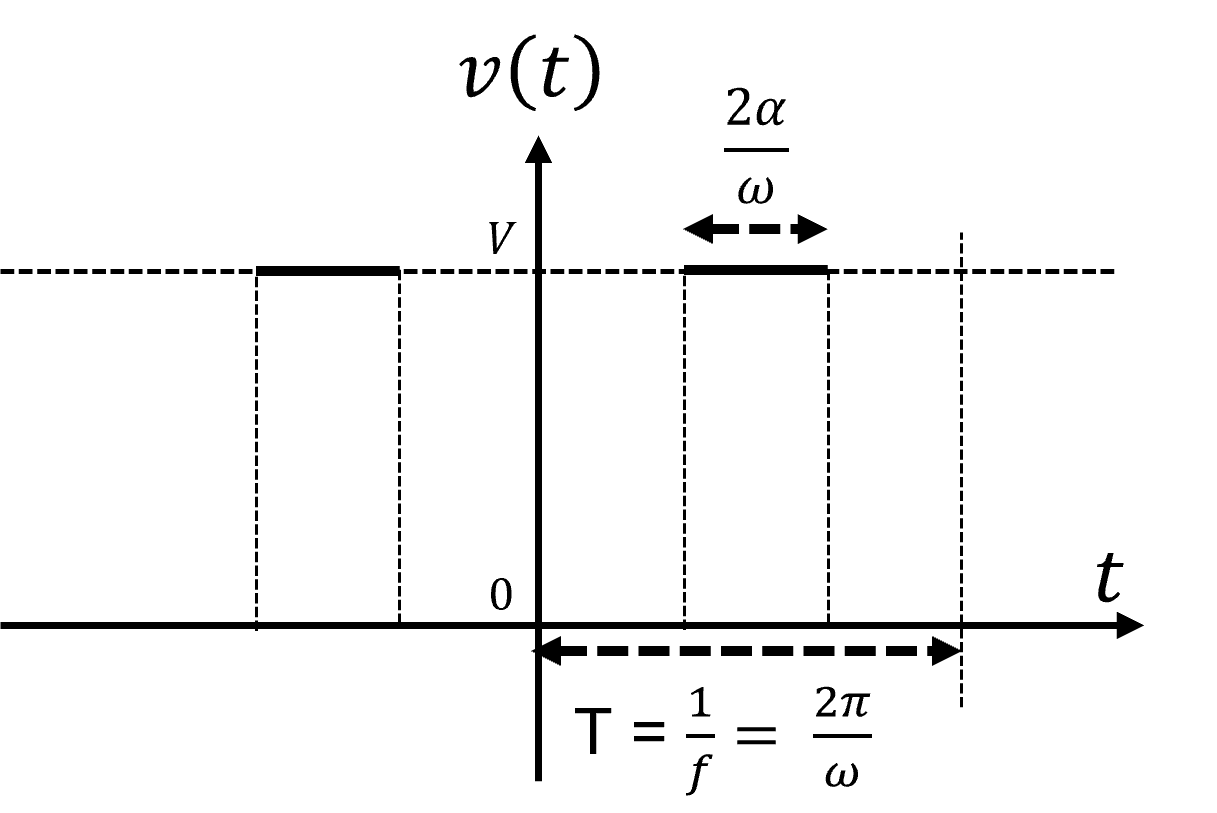
Figura 5(a) - Sinal Pulsado
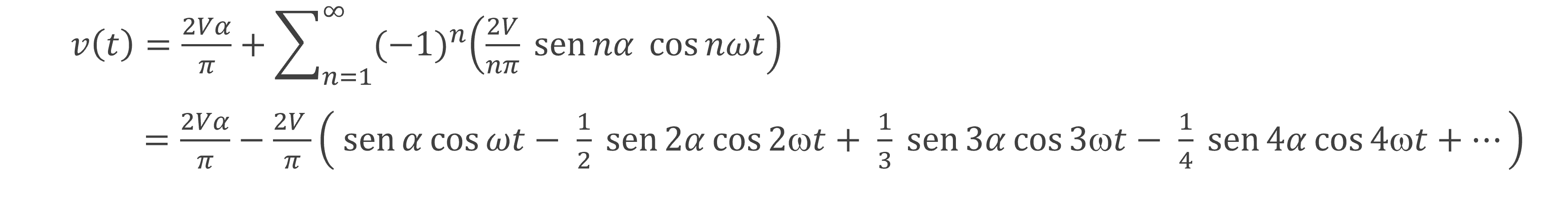
Figura 5(b) - Expressão de Fourier para um Sinal Pulsado
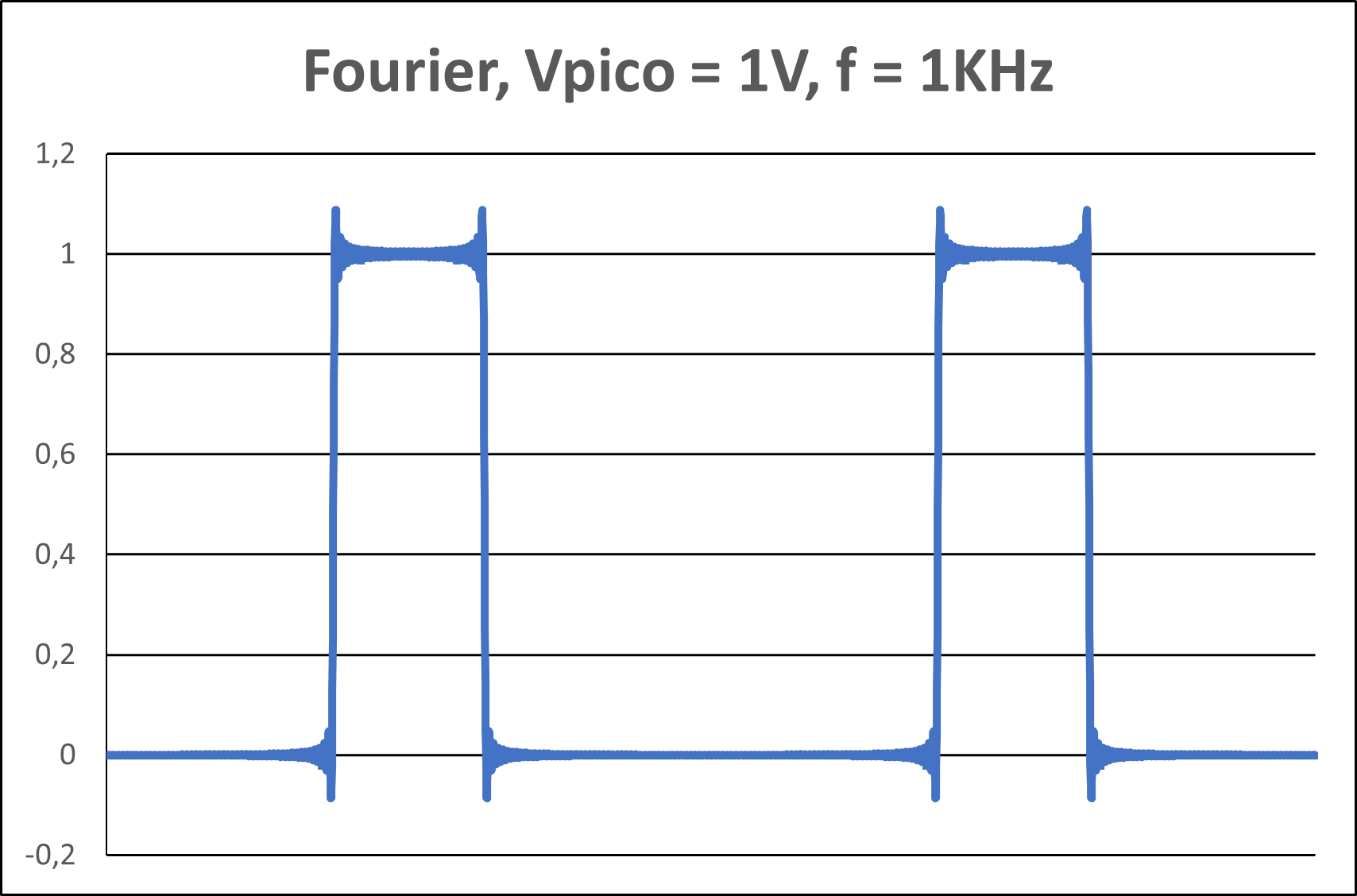
Figura 5(c) - Representação gráfica com 131 harmônicos
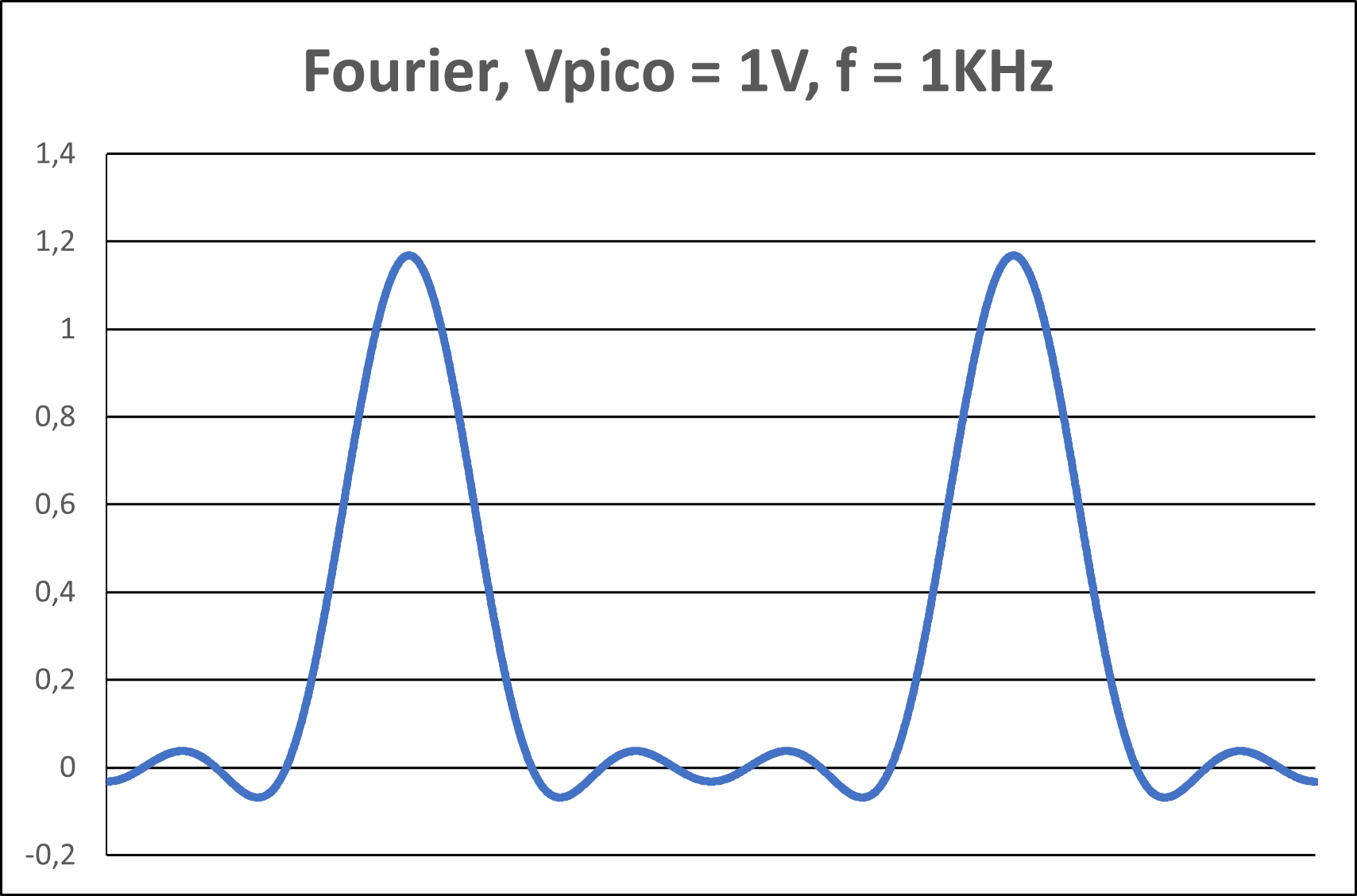
Figura 5(d) - Representação gráfica com 3 harmônicos
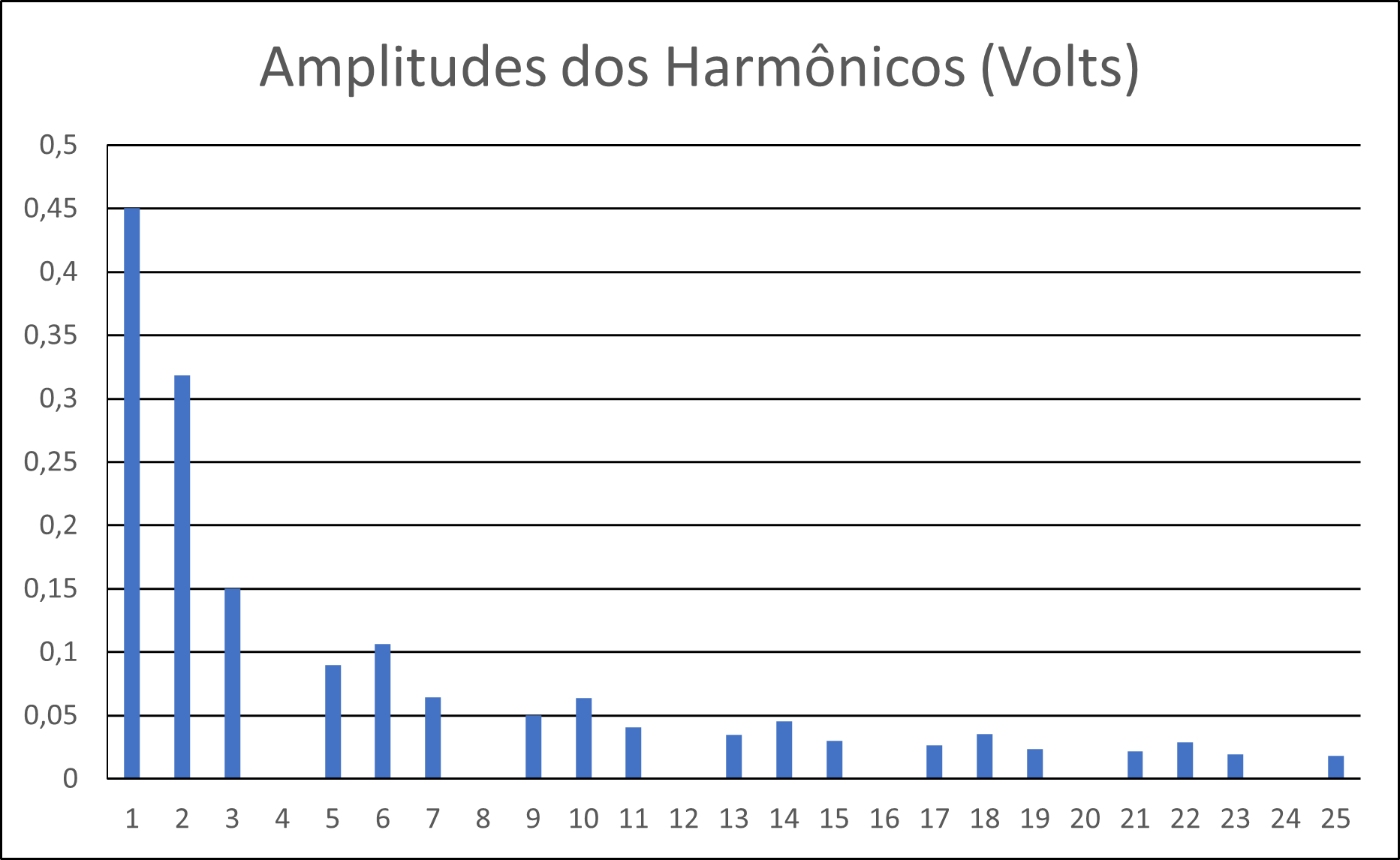
Figura 5(e) - Distribuição dos 25 primeiros harmônicos e suas amplitudes
Seção 6: Filtragem de Sinais
É oportuno discutir o conceito de filtragem de sinais. Filtros são circuitos eletrônicos capazes de eliminar harmônicos de algum sinal a eles aplicados. Um filtro chamado de PASSA-BAIXAS vai eliminar os harmônicos de ordem elevada. Como exemplo, o processamento de uma onda quadrada em um filtro PASSA-BAIXAS vai transformar o sinal original em uma onda, com conteúdo harmônico concentrado nas frequências mais baixas. Como é de se esperar, o sinal resultante perderá a sua característica abrupta e vai se tornar mais suave ou "arredondado". Por outro lado, um filtro PASSA-ALTAS vai eliminar o conteúdo harmônico nas frequências mais baixas, resultando em um sinal mais "nervoso". Um filtro PASSA-FAIXAS, vai se comportar como uma combinação dos filtros PASSA-BAIXAS e PASSA-ALTAS, eliminando os conteúdos harmônicos de ordem mais alta e mais baixa, e mantendo apenas o conteúdo harmônico em uma faixa intermediária de frequências.
Como exemplo, vamos considerar uma onda quadrada, de frequência 10 KHz, aplicada a um filtro PASSA-BAIXAS ideal, com frequencia de corte de 20 KHz. Para este exemplo, qual seria o sinal na saída do filtro?
Uma resposta mais afoita vai indicar que, como a frequência de corte do filtro é superior à do sinal, a onda quadrada não será afetada pelo filtro e vai aparecer na saída exatamente como se apresentou na sua entrada. De fato, não é isso o que vai acontecer... Com efeito, uma onda quadrada É, NA VERDADE, uma soma de várias senoides. Neste exemplo, vamos ter senoides com frequências de 10 KHz ( = 1 x 10 KHz), 30 KHz ( = 3 x 10 KHz), 50 KHz ( = 5 x 10 KHz) e por aí vai... Todas essas senoides serão aplicadas ao filtro, ao mesmo tempo, já que estão todas somadas, exatamente para formar uma onda quadrada. Como se trata de um filtro PASSA-BAIXAS ideal, a senoide de 10 KHz vai passar sem qualquer impacto. Por outro lado, todas as demais serão eliminadas. Assim, o sinal na saída do filtro será uma senoide de frequência 10 KHz. O ferramental de Fourier permite até a determinação da amplitude desta senoide.
Evidentemente, os filtros não são ideais, e, ao processar uma onda quadrada em um filtro prático, a saída não será exatamente uma senoide. O resultado vai depender de diversos fatores tais como o tipo de filtro e a sua ordem. O tema de filtros eletrônicos é bem mais amplo e vai ser abordado de forma mais focada, em outro texto.
Seção 7: Considerações Finais
Voltando à questão da representação de sinais, há que se considerar que, na prática, não existem sinais perfeitos e sempre haverá alguma limitação na implementação física de um sinal. Um primeiro aspecto a se considerar é a questão da perspectiva. Tomando como exemplo uma onda quadrada de frequência fundamental de 1KHz, ao analisar alguns ciclos desta onda na tela de um osciloscópio, têm-se a impressão de que a onda é perfeita. Por outro lado, se a base de tempo for expandida, será possível analisar apenas a variação do nível baixo para o alto (ou o contrário, de acordo com o modo de trigger). Neste caso, vai-se notar que a variação, antes considerada abrupta, agora passa a ser vista de forma bem mais suave que antes. Ou seja, a variação do nível baixo para o nível alto efetivamente não ocorre de forma instantânea, mas de forma relativamente suave. Este comportamento pode se dever tanto à geração da onda quadrada na fonte de sinais, quanto às limitações do osciloscópio em uso, ou ainda à combinação simultânea desses dois fatores.
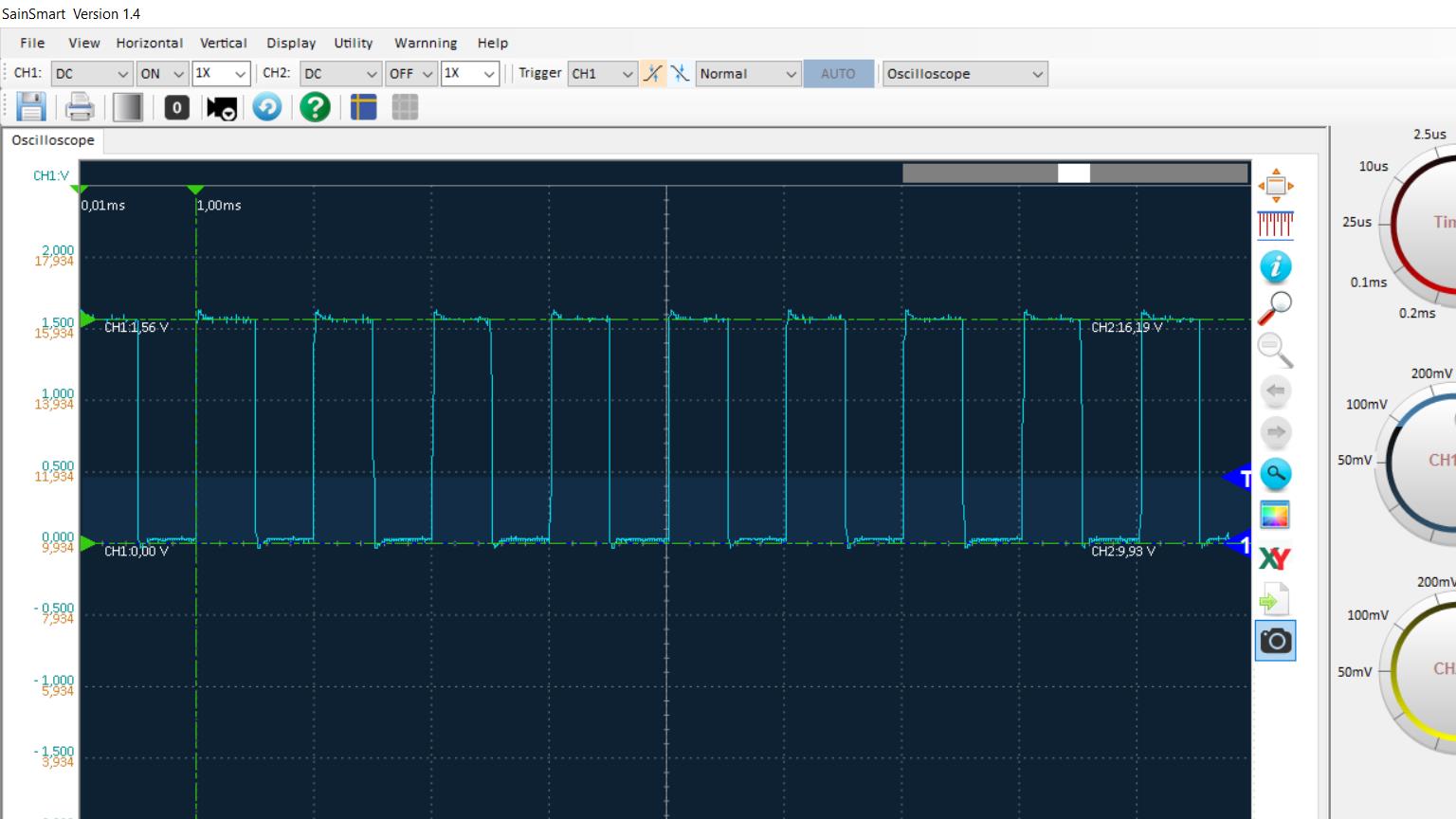
Figura 6(a) - Base de Tempo "fechada"
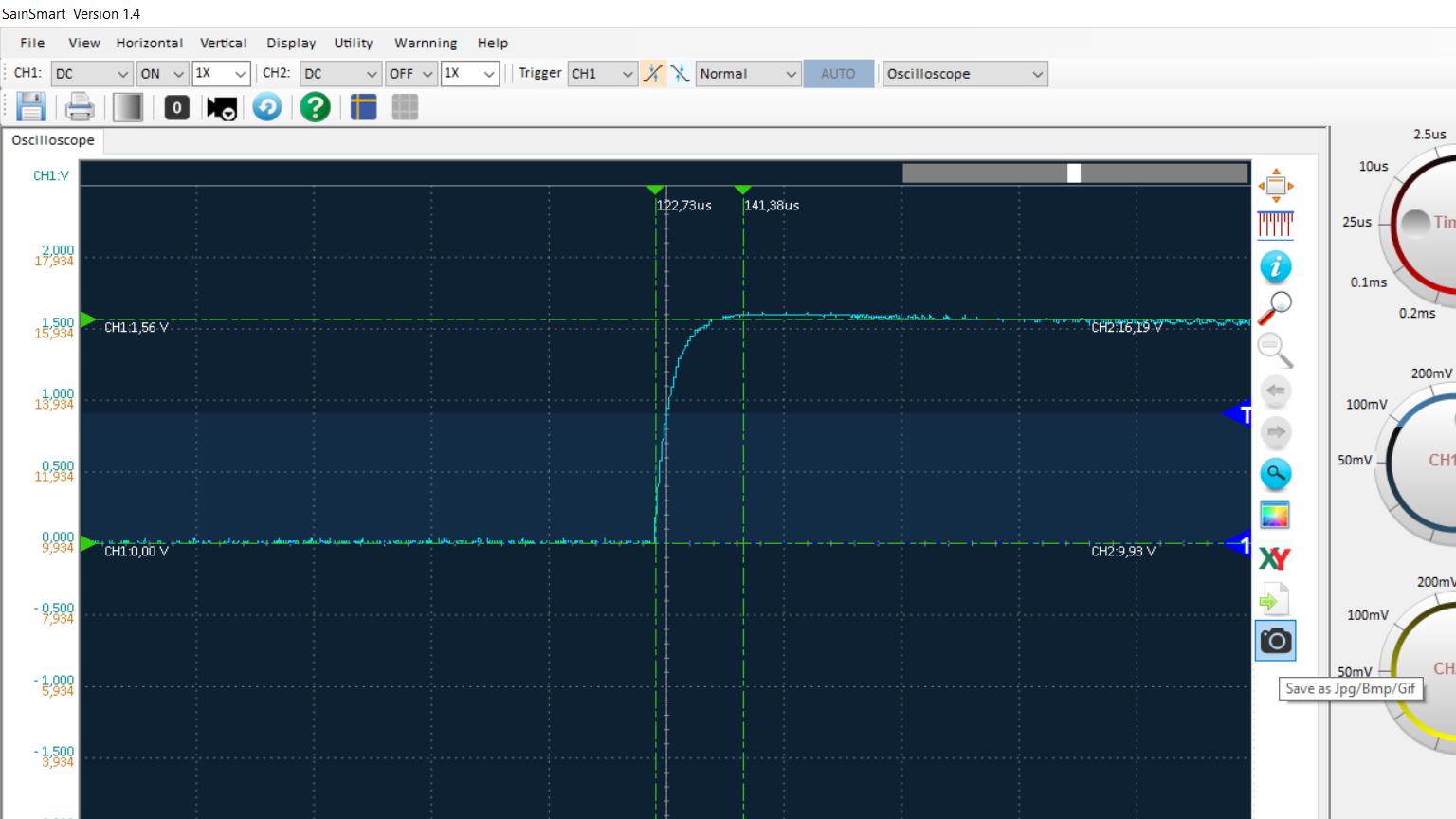
Figura 6(b) - Base de Tempo "aberta"
Outro aspecto a se considerar diz respeito à questão da "inteligibilidade" do sinal. Supondo-se que não será possível trabalhar com infinitos harmônicos, quantos deles serão necessários para que não se perca a informação de que a onda quadrada, de fato, continua quadrada?
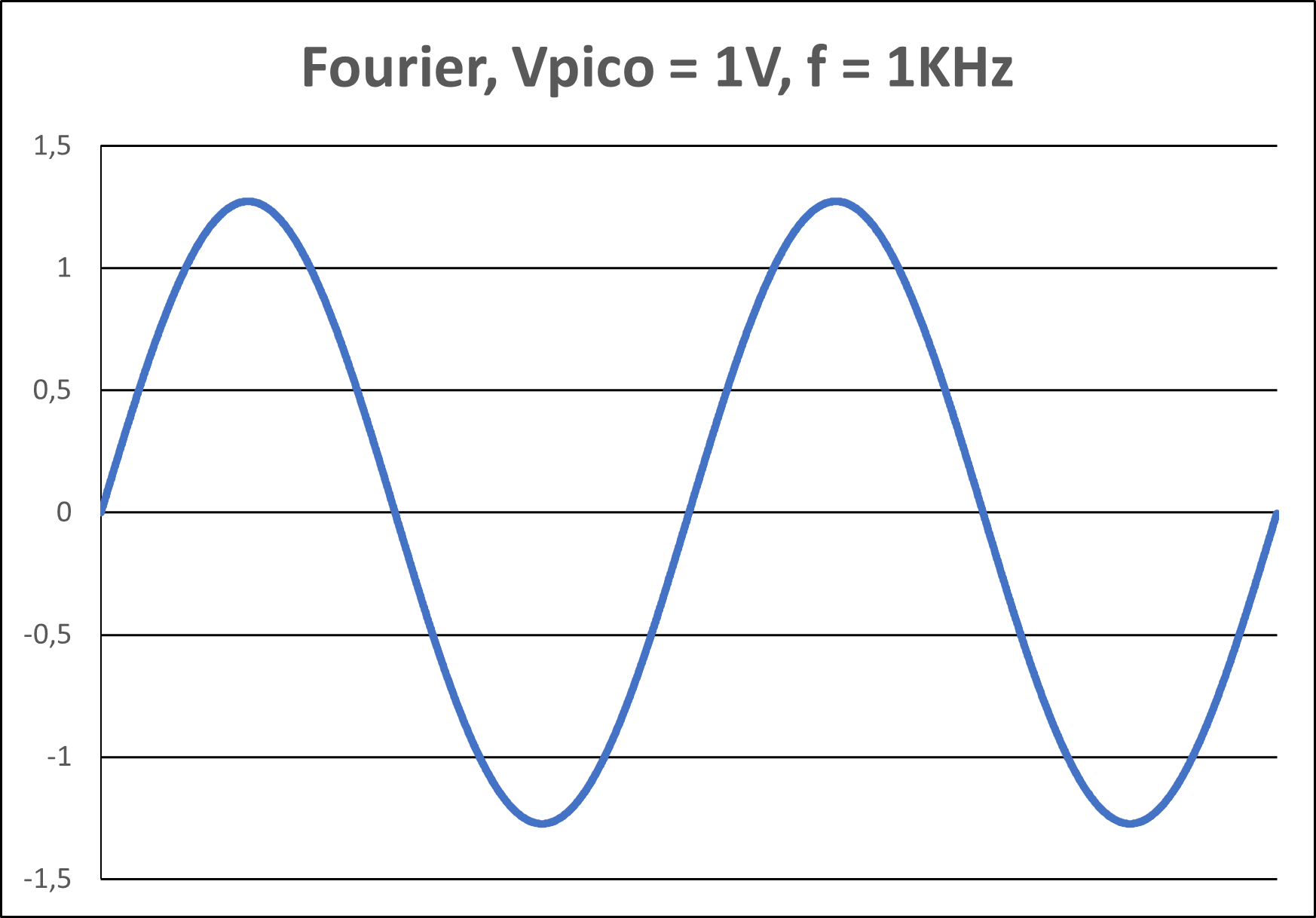
Figura 7(a) - Onda Quadrada - 1 Harmônico
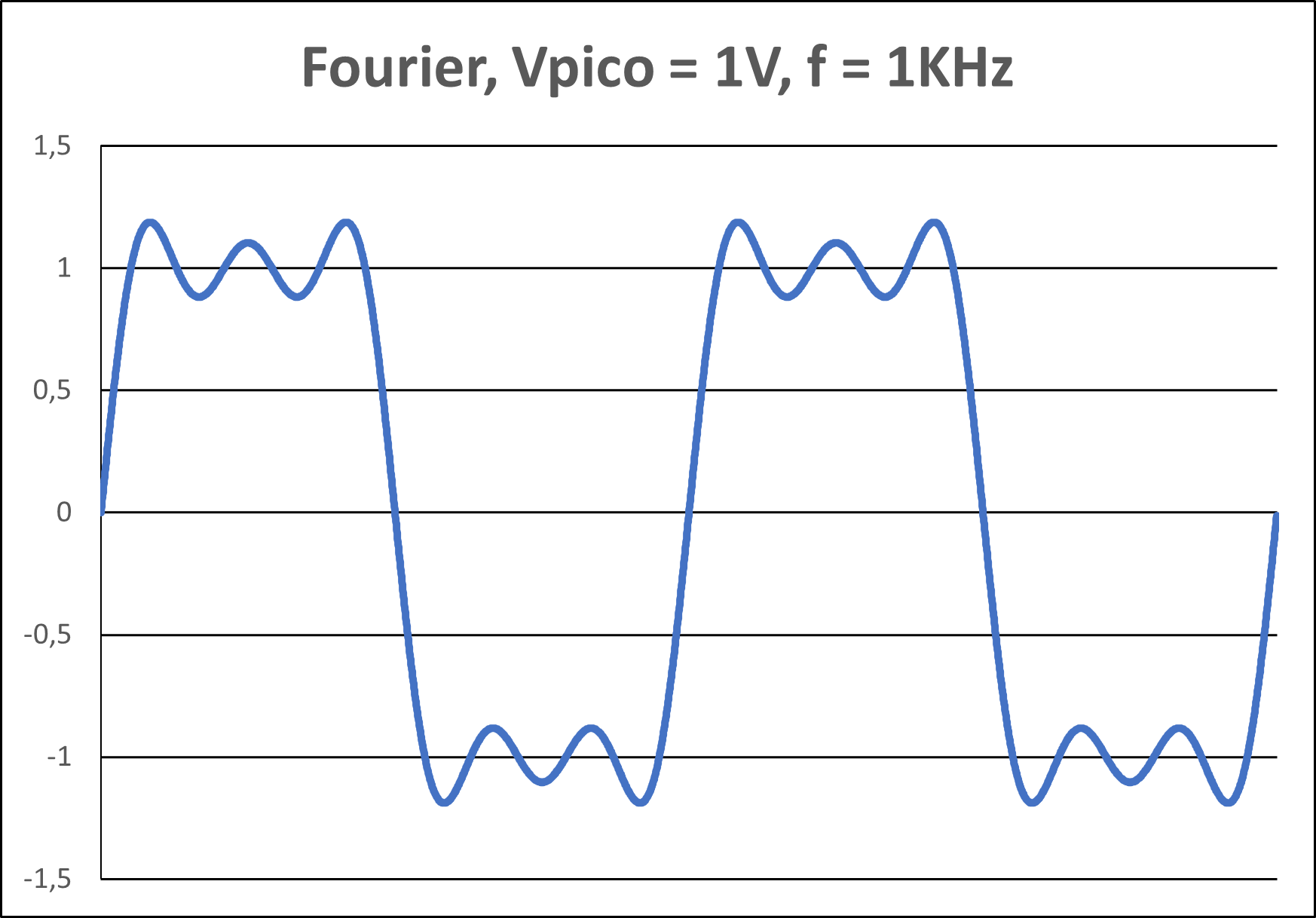
Figura 7(b) - Onda Quadrada - 5 Harmônicos
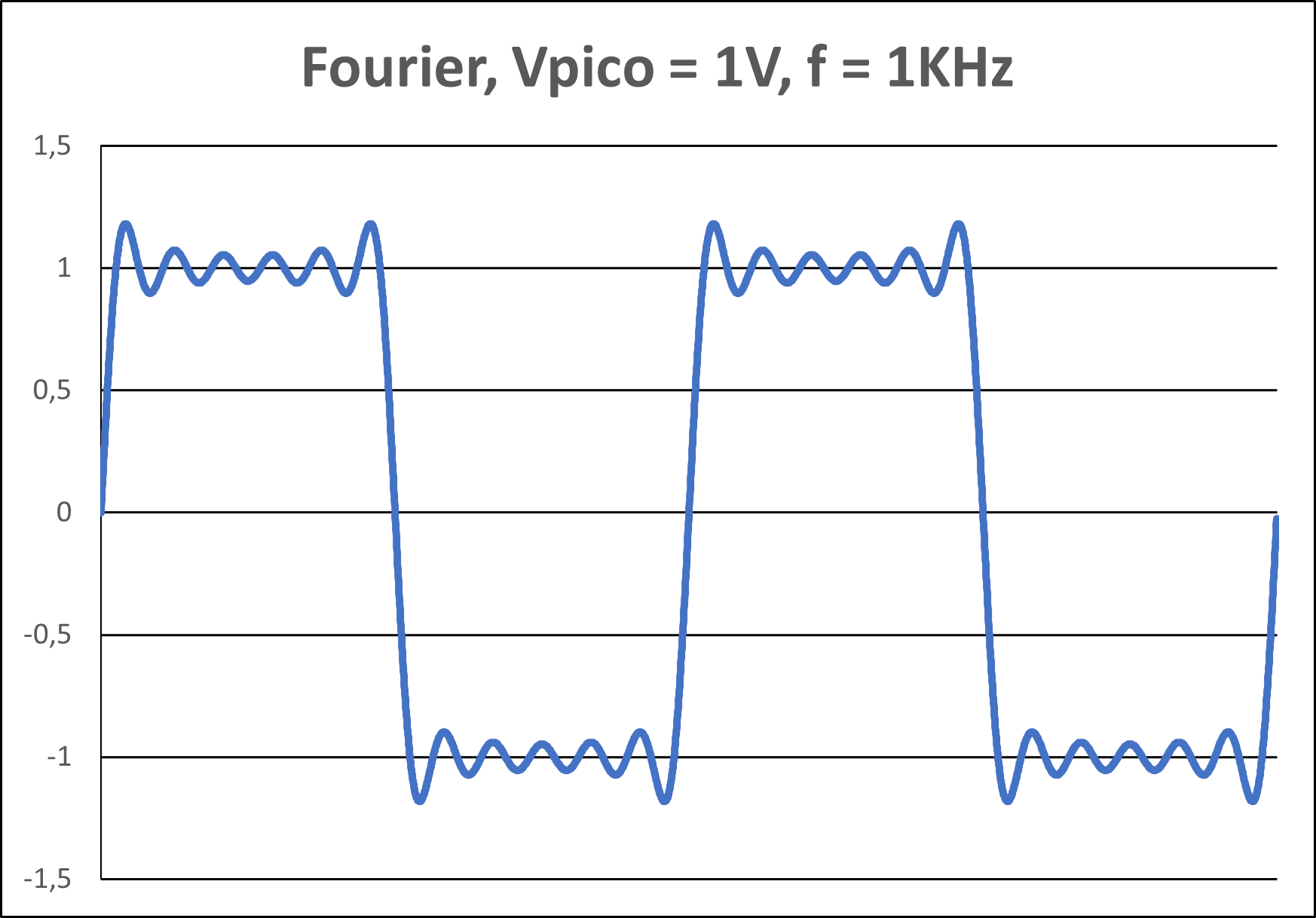
Figura 7(c) - Onda Quadrada - 11 Harmônicos
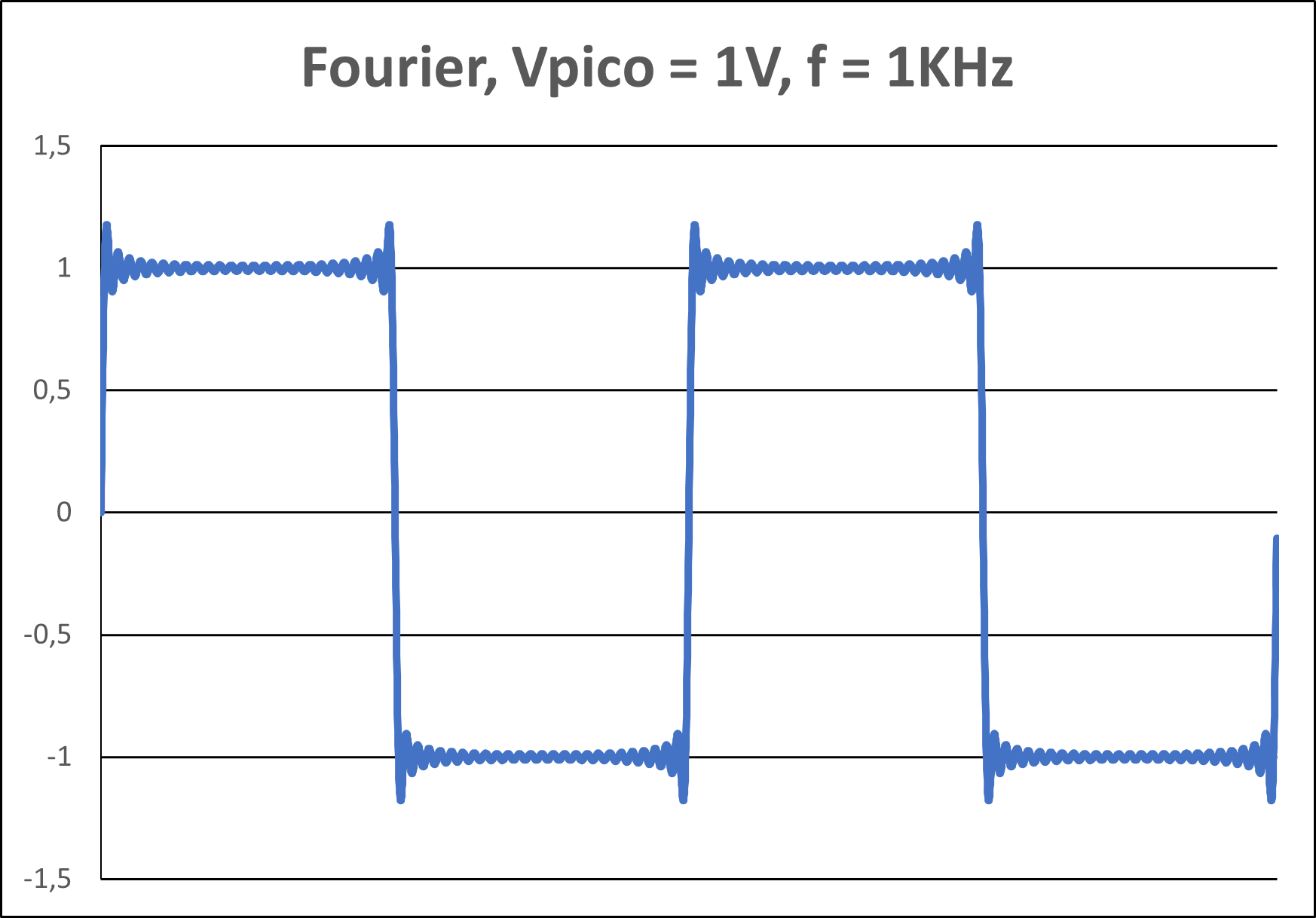
Figura 7(d) - Onda Quadrada - 51 Harmônicos
Como mostrado, o uso de 51 harmônicos representa a onda quadrada de forma bem melhor que se usarmos 1, 5 ou mesmo 11 harmônicos. Por outro lado, considerando uma frequência fundamental de 1KHz, a transmissão de 51 harmônicos vai requerer a transmissão de uma banda de 51KHz. Se a transmissão de apenas 1 ou 5 harmônicos for aceitável, os requisitos de banda serão bem menores. De concreto, a "banda" de um sinal indica exatamente o conteúdo harmônico do sinal em questão.
Do ponto de vista de processamento de sinais, existem diversos tratamentos, absolutamente necessários, visando uma adequada transmissão do sinal. Entre eles, destaca-se o chamado filtro Anti Aliasing. Conforme a definição da Wikipedia, o filtro anti-aliasing (AAF) é usado numa etapa anterior à amostragem do sinal, visando restringir a sua largura de banda, para satisfazer os requisitos do teorema de amostragem de Nyquist-Shannon. Como o teorema afirma, a reconstrução inequívoca do sinal, a partir de suas amostras, só será possível quando a potência das frequências, acima da frequência de Nyquist, é zero. Isto implica em que um sinal a ser amostrado com frequência 2f deve ter uma banda igual ou inferior a f. Outros tratamentos referem-se a operações de compressão ou expansão, correção de fases, e mesmo as modulações em banda base ou de transmissão. Em todos estes cenários haverá algum efeito sobre a banda do sinal e sobre o seu conteúdo harmônico.
Estas questões são muito importantes e prementes, especialmente nos dias de hoje em que a sociedade se tornou altamente dependente de uma comunicação fazendo uso de transmissão de sinais elétricos. De fato, os requisitos de banda de um sinal são determinantes para a escolha do meio físico pelo qual ele pode trafegar. Isto porque, se o meio de transmissão não comportar a banda total necessária, ele vai atuar como um filtro para o sinal em questão. Todos estes aspectos são considerados ao definir um sistema de transmissão de sinais e envolvem a definição das frequências de transmissão, as modulações a serem empregadas, a quantidade de símbolos a serem transmitidos (um símbolo pode ser tanto um nível alto ou baixo como elementos mais complexos tais como diversos níveis, ou frequências, ou fases ou mesmo a combinação destas três grandezas), o meio de transmissão a ser utilizado, e o "overhead" de informação a ser empregado para lidar com aspectos de detecção e correção de erros de transmissão.
Neste contexto, a análise de Fourier constitui-se num aspecto muito importante do estudo e implantação de telecomunicações. A compreensão dos conceitos envolvidos já se constitui num excelente ponto de partida para um maior aprofundamento nos aspectos de projeto, implantação, operação e manutenção dos modernos sistemas de telecomunicações.